Viterbi Algorithm Concept

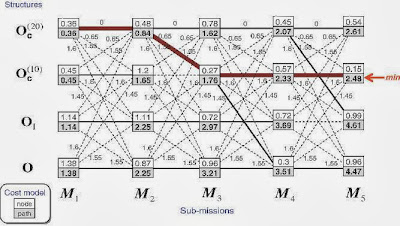
According to the state diagram shown in this link finite state machine, a trellis diagram looks like in the following figure can be built. Each node corresponds to a district state at a given time, and each branch represents a transition to some new states at the next instant of time. The trellis begins and ends at the known state x₀ and x_k. Its most important property is that to every possible state sequence x there corresponds to a unique path through the trellis, and vice versa.

Given a sequence of observations z, every path may be assigned a length proportional to | -ln P(x, z)|, where x is the state sequence associated with that path. This is used to solve the problem of finding the state sequence for which P(x | z) is maximum, or equivalently for which P(x, z) = P(x | z) P(z) is maximum, by finding the path whose length |-ln P(x, z)| is minimum, since ln P(x, z) is a monotonic function of P(x, z) and there is a one-to-one correspondence between paths and sequences (Forney 1973). P(x, z) factor is given as:

Hence, assume if each branch (transition) the length:

Then the total length of the path corresponding to some x is as claimed.

is a segment consists of the states to time k of the state sequence x ≈ (x_0, x_{1, ...,} x_k) and corresponds to a path segment in the trellis starting at the node x₀ and terminating at x_k.
For any particular time-k at node x_k, there will in general be several such path segments, each with some lengths. 

The shortest such path segment is called the survivor corresponding to the node x_k, and denoted

For any time k > 0, there are M survivors in all, one for each x_k. 

The observation is: the shortest completes path must begin with one of the survivors 

Thus at any time-k, we need to remember only M survivor and their lengths 

To get to time k+1, we need only to extend all time-k survivors by one time unit, compute the lengths of the extended path segments, and for each node x_k+1 select the shortest extended path segment terminating in x_k+1 as the corresponding time-(x_k+1) survivor. Recursion proceeds indefinitely without the number of survivors ever exceeding M. 

References:

• Forney, G. D. 1973. The Viterbi algorithm. Proceeding of the IEEE 61: 268-278.

Viterbi Decoding Algorithm

The Viterbi algorithm (VA) is a coding method for mitigating the effect of noise at the receiver. The VA reduces the computational load and complexity by early rejecting the unlikely paths in the coding trellis. The Viterbi decoding algorithm was introduced and analyzed by Andrew J. Viterbi in 1967. Since then, other researchers have expanded on his work by finding good convolutional codes, exploring the performance limits of the technique, and varying decoder design parameters to optimize the implementation of the technique in hardware and software.

The VA is a popular method used to decode convolutionally coded messages. This algorithm tracks down the most likely state sequences of the encoder went through in decoding the message, and uses this information to determine the original message. Instead of estimating a message based on each individual sample in the signal, the convolutional encoding and Viterbi decoding process packages and encodes a message as sequence, providing a level of correlation between each sample in the signal (Davis et al. 2002).

The VA fits nicely into the streaming paradigm. For a 1/2 rate VD, a stream of two-bit digital elements is input into the VD, and a stream of one-bit element is returned. The decoding process involves two major steps: metric update and traceback. These two steps can be thought of as kernels. An illustration on how these two kernels might interconnect with input and output streams is shown in the following figure (the figure under contruction).